So funktioniert die Annäherungssuche

So funktioniert die Annäherungssuche

Annäherungssuche

Dies ist eine Analogie zur binären Suche, jedoch ohne deren Einschränkungen, dass gesuchte Funktion/Wert/Parameter streng monotone Funktionen sein müssen, während sie den O(log(n)) teilen Komplexität.

Nehmen wir zum Beispiel folgendes Problem an

Wir kennen die Funktion y=f(x) und x0 finden möchten so dass y0=f(x0) . Dies kann grundsätzlich durch Umkehrfunktion zu f erfolgen aber es gibt viele Funktionen, von denen wir nicht wissen, wie man sie invers berechnet. Wie berechnet man das in einem solchen Fall?

bekannt

y=f(x) - Eingabefunktion
y0 - gesuchter Punkt y Wert
a0,a1 - Lösung x Intervallbereich

Unbekannt

x0 - gesuchter Punkt x Der Wert muss im Bereich x0=<a0,a1> liegen

Algorithmus

prüfen Sie einige Punkte x(i)=<a0,a1> gleichmäßig entlang der Strecke mit einem Schritt da verteilt

Also zum Beispiel x(i)=a0+i*da wobei i={ 0,1,2,3... }
für jeden x(i) Berechnen Sie den Abstand/Fehler ee des y=f(x(i))

Dies kann beispielsweise so berechnet werden:ee=fabs(f(x(i))-y0) Es können aber auch alle anderen Metriken verwendet werden.
Denken Sie an Punkt aa=x(i) mit minimalem Abstand/Fehler ee
Stopp bei x(i)>a1
Genauigkeit rekursiv erhöhen

Beschränken Sie also zuerst den Bereich, um nur um die gefundene Lösung herum zu suchen, zum Beispiel:
```
a0'=aa-da;
a1'=aa+da;
```
Erhöhen Sie dann die Genauigkeit der Suche, indem Sie den Suchschritt verringern:
```
da'=0.1*da;
```
wenn da' nicht zu klein ist oder die maximale Rekursionszahl nicht erreicht ist, gehen Sie zu #1
gefundene Lösung ist in aa

Folgendes habe ich im Sinn:

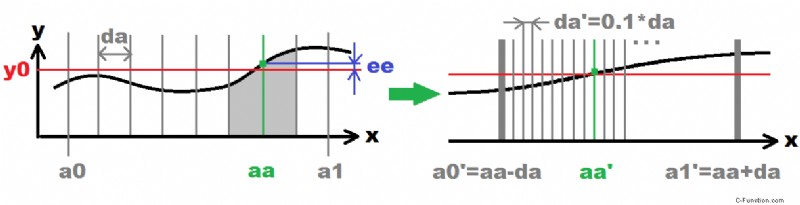
Auf der linken Seite ist die anfängliche Suche dargestellt (Aufzählungszeichen #1, #2, #3, #4 ). Auf der rechten Seite die nächste rekursive Suche (Punkt #5 ). Dies wird eine rekursive Schleife durchlaufen, bis die gewünschte Genauigkeit erreicht ist (Anzahl der Rekursionen). Jede Rekursion erhöht die Genauigkeit um 10 Mal (0.1*da ). Die grauen vertikalen Linien stellen das untersuchte x(i) dar Punkte.

Hier der C++-Quellcode dafür:

//---------------------------------------------------------------------------
//--- approx ver: 1.01 ------------------------------------------------------
//---------------------------------------------------------------------------
#ifndef _approx_h
#define _approx_h
#include <math.h>
//---------------------------------------------------------------------------
class approx
    {
public:
    double a,aa,a0,a1,da,*e,e0;
    int i,n;
    bool done,stop;

    approx()            { a=0.0; aa=0.0; a0=0.0; a1=1.0; da=0.1; e=NULL; e0=NULL; i=0; n=5; done=true; }
    approx(approx& a)   { *this=a; }
    ~approx()           {}
    approx* operator = (const approx *a) { *this=*a; return this; }
    //approx* operator = (const approx &a) { ...copy... return this; }

    void init(double _a0,double _a1,double _da,int _n,double *_e)
        {
        if (_a0<=_a1) { a0=_a0; a1=_a1; }
        else          { a0=_a1; a1=_a0; }
        da=fabs(_da);
        n =_n ;
        e =_e ;
        e0=-1.0;
        i=0; a=a0; aa=a0;
        done=false; stop=false;
        }
    void step()
        {
        if ((e0<0.0)||(e0>*e)) { e0=*e; aa=a; }         // better solution
        if (stop)                                       // increase accuracy
            {
            i++; if (i>=n) { done=true; a=aa; return; } // final solution
            a0=aa-fabs(da);
            a1=aa+fabs(da);
            a=a0; da*=0.1;
            a0+=da; a1-=da;
            stop=false;
            }
        else{
            a+=da; if (a>a1) { a=a1; stop=true; }       // next point
            }
        }
    };
//---------------------------------------------------------------------------
#endif
//---------------------------------------------------------------------------

So wird es verwendet:

approx aa;
double ee,x,y,x0,y0=here_your_known_value;
//            a0,  a1, da,n, ee  
for (aa.init(0.0,10.0,0.1,6,&ee); !aa.done; aa.step())
    {
    x = aa.a;        // this is x(i)
    y = f(x)         // here compute the y value for whatever you want to fit
    ee = fabs(y-y0); // compute error of solution for the approximation search
    }

in der rem oben for (aa.init(... sind die genannten Operanden. Der a0,a1 ist das Intervall, in dem der x(i) wird untersucht, da ist der erste Schritt zwischen x(i) und n ist die Anzahl der Rekursionen. also wenn n=6 und da=0.1 der letzte maximale Fehler von x fit wird ~0.1/10^6=0.0000001 sein . Der &ee ist ein Zeiger auf eine Variable, in der der tatsächliche Fehler berechnet wird. Ich wähle Zeiger, damit es beim Verschachteln keine Kollisionen gibt und auch aus Geschwindigkeitsgründen, da das Übergeben von Parametern an stark genutzte Funktionen Heap-Trashing verursacht.

[Notizen]

Diese Annäherungssuche kann in jede Dimensionalität verschachtelt werden (aber grob muss man auf die Geschwindigkeit achten), siehe einige Beispiele

Annäherung von n Punkten an die Kurve mit der besten Anpassung
Kurvenanpassung mit y-Punkten an wiederholten x-Positionen (Galaxy-Spiralarme)
Zunehmende Genauigkeit der Lösung der transzendenten Gleichung
Finden Sie eine Ellipse mit minimaler Fläche, die eine Reihe von Punkten in C++ umschließt
2D TDoA Zeitdifferenz der Ankunft
3D TDoA Zeitdifferenz der Ankunft

Im Falle einer Nichtfunktionsanpassung und der Notwendigkeit, "alle" Lösungen zu erhalten, können Sie die rekursive Unterteilung des Suchintervalls nach der gefundenen Lösung verwenden, um nach einer anderen Lösung zu suchen. Siehe Beispiel:

Wie berechne ich bei gegebener X-Koordinate die Y-Koordinate für einen Punkt, sodass er auf einer Bezier-Kurve ruht?

Was sollten Sie beachten?

Sie müssen das Suchintervall <a0,a1> sorgfältig wählen es enthält also die Lösung, ist aber nicht zu breit (sonst wäre es langsam). Auch Anfangsschritt da ist sehr wichtig, wenn es zu groß ist, können Sie lokale Min/Max-Lösungen verpassen, oder wenn es zu klein ist, wird das Ding zu langsam (insbesondere für verschachtelte mehrdimensionale Anpassungen).